Here's Some Free Math Tools For You - Notebooks
Use them in your classroom or homeschool lessons

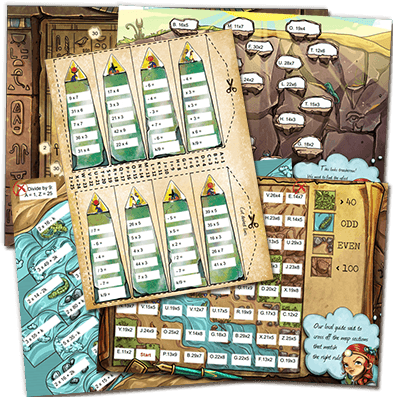
Free Printable Math Notebook and Math Tools
Best for grades second through sixth. Includes over 80 pages of fill-in math vocabulary and dozens math tools. Print one page or print them all and, of course, free!
MathNotebook |
||
|
||
|
Why Math Notebooks? Math Notebooks or Math Journals are a students companion, guide and reflection journal through out their school year. It is a place where they record thoughts about math, reflect on learning, workout and practice problems, build their math vocabulary. In addition it is a resource of math tools to aid their problem solving. Students self-discovery is accomplished in their problem solving which is a key component of the Math Common Core. Suggestions for Setting up Math Notebook Request a 1 1/2 inch binder and four dividers for school supplies from parents and/or sell the need to your administration.You can also request 5 dividers or make them with students. Print, copy back-to-back, use a electronic hole puncher (try the office, you never know!). Start the notebook ASAP. They leave the notebook in class, unless you have angels. Sections: 1.Problem Solving or Problem of the Day. 2. Class Work or Independent Practice. 3. Notes. 4.Reflections. 5.Vocabulary. 6.Math Tools. Best print view: Explorer This math notebook or math journal is best for 3rd-5th grade. You can supplement for second and sixth grade. We will do are best to bring you free Math Notebooks for each grade at a later date.
|
| TheTeachers
Cafe |
Best for grades two through sixth. It includes over 80 pages of fill-in math vocabulary and dozens of math tools. Print the whole notebook, or just one math tool.
Your Next Lesson Is Already Done.
Treat yourself to an easy lesson with a classroom-ready, curriculum-aligned activity kit.
Each classroom activity works by transforming the lesson into an engaging game that gets students invested.
You'll spark your students creativity, develop their critical thinking, and reclaim a little breathing space all in one genius move.
Just download a kit, print it out and instantly become the cool teacher!
Covers many Common Core Standards including: CCSS.Math.Content.1.OA.B.3 Apply properties of operations as strategies to add and subtract.2 Examples: If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of addition.) To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition.)
CCSS.Math.Content.2.NBT.B.5 Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
CCSS.Math.Content.2.NBT.B.6 Add up to four two-digit numbers using strategies based on place value and properties of operations.
CCSS.Math.Content.2.NBT.B.7 Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
CCSS.Math.Content.3.OA.B.5 Apply properties of operations as strategies to multiply and divide.2 Examples: If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × 2 = 10, then 3 × 10 = 30. (Associative property of multiplication.) Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.)
CCSS.Math.Content.3.OA.B.6 Understand division as an unknown-factor problem. For example, find 32 ÷ 8 by finding the number that makes 32 when multiplied by 8.
CCSS.Math.Content.3.OA.C.7 Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
CCSS.Math.Content.4.OA.A.1 Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 × 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
CCSS.Math.Content.4.NF.C.5 Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100.2 For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
CCSS.Math.Content.4.NF.C.6 Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
CCSS.Math.Content.4.NF.C.7 Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.
CCSS.Math.Content.4.OA.B.4 Find all factor pairs for a whole number in the range 1–100. Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range 1–100 is a multiple of a given one-digit number. Determine whether a given whole number in the range 1–100 is prime or composite.
CCSS.Math.Content.4.NF.B.3 Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
CCSS.Math.Content.4.NF.B.3a Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
CCSS.Math.Content.4.NF.B.3b Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.