Printable Benchmark Fractions, Decimals and Percents

 
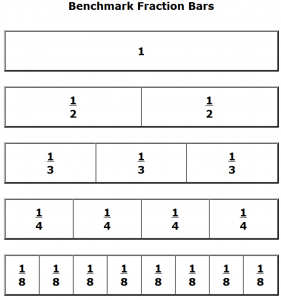
Fraction, Decimal, Percent Bars  - Free Printable Fraction, Decimal, Percent Bars. Great for comparing or converting. You can put the up on the Elmo or the Smart Board.

Smart Board Fraction Strips - You can use the electronic worksheets on the Smart Board, or you can use these colored fractions for a better look.

CCSS.Math.Content.3.NF.A.3b Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
CCSS.Math.Content.3.NF.A.3 Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
Extend understanding of fraction equivalence and ordering.
CCSS.Math.Content.4.NF.A.1 Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
CCSS.Math.Content.4.NF.A.2 Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model. Build fractions from unit fractions. CCSS.Math.Content.4.NF.B.3 Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
CCSS.Math.Content.4.NF.B.3a Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
CCSS.Math.Content.4.NF.B.3b Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.
CCSS.Math.Content.4.NF.B.3c Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
CCSS.Math.Content.4.NF.B.3d Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
Understand decimal notation for fractions, and compare decimal fractions.
CCSS.Math.Content.4.NF.C.5 Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100.2 For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
CCSS.Math.Content.4.NF.C.6 Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
CCSS.Math.Content.4.NF.C.7 Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.
CCSS.Math.Content.5.NF.B.6 Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
CCSS.Math.Content.6.RP.A.3c Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.